네트워크 플로우 Network Flow
-
특정 지점에서 다른 지점으로 데이터가 얼마나 많이 흐르고 있는지 측정하는 알고리즘
⇒ 최대 유량 max flow 문제 해결에 사용되는 알고리즘
-
example

- A→D의 최대 유량은 6, 6 이상을 보내면 정체 현상이 발생하기 때문이다.
- 각 경로의 용량 중 가장 작은 것이 최대 유량
- Terminologies
- flow: 두 정점 사이에서 현재 흐르는 양
- capacity: 두 정점 사이에서 최대로 흐를 수 있는 양
- source: 유량이 시작되는 정점
- sink: 유량이 도착하는 정점
- augumenting path: 소스에서 싱크로 유량을 보내는 경로
- residual capacity: 용량 - 유량
- Properties
- 용량 < 유량 (capacity < flow)
-
flow(m,n) = -flow(n,m)
m→n 유량 = -(n→m 유량) 과 같음
- 용량 < 유량 (capacity < flow)
에드몬드-카프 Edmonds-Karp
- BFS 이용
- 가능한 모든 경우의 수를 탐색하여 최대 유량 계산
- example

- flow / capacity
- 현재 유량을 모두 0으로 초기화 ⇒ 0/capacity
- 여기서 capacity 내에서 가능한 용량의 양을 반복적으로 더해준다.

-
1→2→3→6 경로에서 흐를 수 있는 최대 유량은 6
→ 각 경로의 flow에 6씩 더해줌

-
1→2→6 경로에서 가능한 최대 flow = 6
→ 각 경로에 6씩 더해준다.
-
1→2 경로의 flow가 capa에 도달
-
위와 같은 방식으로 1→4→5→6, 1→4→5→3→6 경로의 유량을 갱신한다.
-
더이상 1→6 새로운 경로가 없을때까지 반복
-
음의 유량 계산하기
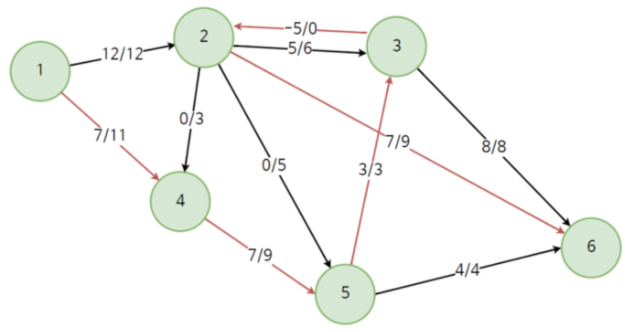
-
2→3 : 6/6
⇒ 3→2 : -6/0 을 의미
-
다음 예시에서 1→6의 최대 유량은 1→2→6 (12+7) = 19
포드 풀커슨 Ford-Fulkerson
- DFS 이용
- 가능한 모든 경우의 수를 탐색하여 최대 유량 계산
References
- 성균관대학교 소프트웨어학과 조대호 교수님 2020년도 2학기 알고리즘개론 수업
'컴퓨터 공학 > 알고리즘' 카테고리의 다른 글
| 힙 Heap 개념,우선순위 큐를 이용한 구현 (python)과 성능 비교, 힙 정렬, 상향식 힙 생성, 응용 문제 (0) | 2021.04.09 |
|---|---|
| 위상 정렬 Topology Sort (0) | 2021.02.15 |
| 최단 경로 찾기 Shortest path, 변 경감 edge relaxation, 벨만-포드 Bellam-Ford's, 다익스트리 Dijikstra's 알고리즘 (0) | 2021.02.15 |
| 최소 신장 트리 Minimum Spanning Tree, 크루스칼 Kruskal's, 프림 Prim's 알고리즘 (0) | 2021.02.15 |
| 다이나믹 프로그래밍 Dynamic Programming (0) | 2021.02.15 |



