최단 경로 찾기 Shortest Path
- 두 노드를 잇는 가장 짧은 경로 찾기
- weighted graph에서 엣지 가중치의 합이 최소가 되는 경로 찾기
-
problems
-
single source
단일 노드에서 출발하여 그래프 내의 모든 다른 노드에 도착하는 가장 짧은 경로 찾는 문제
-
single destination
모든 노드에서 출발하여 그래프 내의 한 단일 노드로 도착하는 가장 짧은 경로를 찾는 문제
-
single pair
주어진 꼭지점u, v 사이의 최단 경로 찾는 문제
-
all pair
그래프 내의 모든 노드 쌍 사이의 최단 경로 찾는 문제
-
-
Floyd-Warshall algorithm
- all-pair 최단 경로 문제 알고리즘
- optimal substructure 활용

-
optimal substructure
최단 경로의 부분 경로 역시 최단 경로이다.
-
직선은 엣지, 물견선은 경로, 숫자는 가중치
-
엣지 가중치의 합이 최소인 최단 경로는 5+25 (굵은 선)
-
시작 노드와 중간 노드까지의 중간 경로 역시 5, 25가 최단 경로
-
Proof
-
최단 경로를 decomposition
→ 부분 경로의 합
-
-
최단 경로가 최단 부분 경로로 construct
→ optimal substructure
⇒ dynamic programming, greedy algorithm 활용
변 경감 Edge Relaxaton
-
최단 경로 구하는 알고리즘의 기본 연산
-
시작 노드 s에서 임의의 노드 z까지의 최단 경로 구하는 경우
→ d(z)=75, d(u)=50이라 가정
→ 탐색 중 엣지 e를 경유하는 경로의 거리가 60이면 d(z)는 더이상 최단 경로가 아니게 된다.
⇒ 최단경로를 구성하는 노드와 엣지 정보, 거리 합을 업데이트
-
최단 경로 구성 엣지 가중치의 합을 줄여나간다 (relaxation)
벨만 포드 알고리즘 Bellman-Ford's algorithm
-
concept
-
optimal substructure 활용
$D(s,v) = D(s,u) + w(u,v)$
s에서 v까지의 최단 경로는 s에서 u까지의 최단 경로에 u와 v 사이의 가중치를 더한 값
-
s와 u 사이의 최단 경로를 구할 때 그래프 내의 모든 엣지에 대해edge relaxation을 수행
-
-
Example
-
첫번째 edge relaxation

-
(BE) : 무한대-2=무한대 이므로 업데이트 X
-
... (CD)
-
(AB) = 8 < 무한대
⇒ B에 8 기록
-
(AC) = -2 < 무한대
⇒ C에 -2 기록
-
(AD) = 4 < 무한대
⇒ D에 4 기록
- 두번째 edge relaxation

-
(BE) = 8+(-2) = 6 < 무한대
→ E에 6 기록
-
(CE) = (-2)+3=1 < 6
→ E에 1 기록
-
(FC) = 무한대 + 9 > -2
→ 업데이트 X
-
(DF) = 4+5=9 < 무한대
→ F에 9 기록
-
(CB) = -2+7 = 5 < 8
→ B에 5 기록
-
(CD) = (-2)+1 = -1 < 4
→ D에 -1 기록
-
나머지 update X
- 시작 노드를 제외한 전체 노드 수 만큼 edge relaxation 수행
-
negative cycle
- 가중치가 음수인 경우에도 적용 가능
- 음수 가중치가 사이클을 이루는 경우 불가능
- (ef)의 경우 사이클을 돌수록 거리가 작아져서 최단 경로 구하기 불가능

-
Algorithm
-
모든 엣지에 대해 edge relaxation을 시작 노드를 제외한 전체 노드 수만큼 반복 수행
-
마지막으로 그래프 모든 엣지에 대해 edge relaxation 1번 수행
-
마지막 edge relaxation 중 한번이라도 업데이트가 발생하면 negative cycle이 존재한다는 의미
→ false 반환 후 종료
-

- 시간복잡성 : O(VE) = O(V^3)
다익스트라 알고리즘 Dijikstra's Algorithm
-
concept
-
BFS 기반
-
엣지의 가중치가 음수일 경우 동작하지 않음
-
-
Example
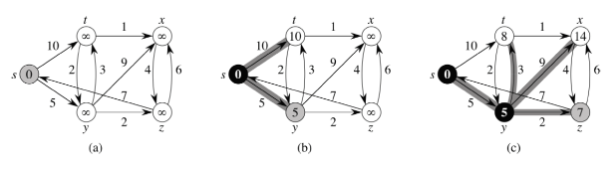
방문 노드 gray, 방문 완료 노드 black, 방문하지 않은 노드 white
-
(b) : 시작 노드 s를 기준으로 BFS 적용
→ s의 형제 노드 t, y의 거리 정보 업데이트
→ t,y 중 가중치가 작은 y를 선택 후 gray로 칠함, s는 black 으로 칠함
-
(c) : y의 형제 노드 t, x, z 거리정보 업데이트
→ 최단 거리인 t를 선택
→ t의 거리 정보 10 > 5+3 (8) 이므로 8로 업데이트
→ edge relaxation : s→t 지우고 s→y→t 경로 살리기
→ 다음 탐색 노드로 z 선택 후 gray로 칠함

-
(d) : z의 형제 노드 y, x 거리 정보 업데이트
→ y는 이미 black이므로 건너뜀
→ x의 거리 정보 13 > 5+3+1(9)
⇒ edge relaxation
→ z black, t gray
-
(e) : t 의 형제노드 x 거리 정보 업데이트 ...
-
모든 노드 방문하면 알고리즘 종료
-
algorithm

- 시간복잡성 : O(V^2)
References
- 성균관대학교 소프트웨어학과 조대호 교수님 2020년도 2학기 알고리즘 수업
'컴퓨터 공학 > 알고리즘' 카테고리의 다른 글
| 위상 정렬 Topology Sort (0) | 2021.02.15 |
|---|---|
| 네트워크 플로우 Network Flow, 에드몬드-카프 Edmonds-Karp, 포드 풀커슨 Ford-Fulkerson 알고리즘 (0) | 2021.02.15 |
| 최소 신장 트리 Minimum Spanning Tree, 크루스칼 Kruskal's, 프림 Prim's 알고리즘 (0) | 2021.02.15 |
| 다이나믹 프로그래밍 Dynamic Programming (0) | 2021.02.15 |
| 분할정복 Divide & Conquer 알고리즘, 합병정렬 Merge Sort 이해하기 (0) | 2021.02.10 |


