분할 정복 Divide and Conquer : 행렬 곱셈 matrix multiplication
-
problem
Program the divide and conquer matrix multiplication using 1) standard algorithm 2) recursion
- For the two cases 1) and 2), Compare the number of computations (multiplication, addition, and subtraction) between 1), 2) cases. In the matrix computation of C = A×B, matrices A and B are filled with rand()%1000, execute srand(time(NULL)) first. (Avoid same values when generating the values randomly.)
- For the case 2) print whenever a partial matrix (except 1×1) of C is constructed, that is, whenever a return value from a recursion is determined, until the completion of the matrix multiplication.
- Execute with the 4x4 matrix multiplication and the 8x8 matrix multiplication. (Print matrices, A, B, and C.)
standard algorithm (no recursion)
-
standard algorithm source code
#define _CRT_SEUCRE_NO_WARNINGS
#include <stdio.h>
#include<stdlib.h>
#include<time.h>
#define N 8
int fill(int **A, int **B) {
int i, j;
srand((unsigned)time(NULL));
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
A[i][j] = rand() % 1000;
}
}
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
B[i][j] = rand() % 1000;
}
}
return 0;
}
int print(int **List) {
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
printf("%d ", List[i][j]);
}
printf("\n");
}
return 0;
}
int standard(int **A, int **B, int **C) {
int i, j, k;
int computation = 0;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
C[i][j] = 0;
for (k = 0; k < N; k++) {
C[i][j] += A[i][k] * B[k][j];
computation++;
}
}
}
print(C);
printf("\n");
printf("the number of computation : %d\n", computation);
return 0;
}
int main() {
int **A = (int**)malloc(sizeof(int) * N);
int **B = (int**)malloc(sizeof(int) * N);
int **C = (int**)malloc(sizeof(int) * N);
for (int t = 0; t < N; t++) {
A[t] = (int*)malloc(sizeof(int) * N);
B[t] = (int*)malloc(sizeof(int) * N);
C[t] = (int*)malloc(sizeof(int) * N);
}
printf("*****Matrix Multiplication*****\n\n");
printf(" (a) Compare 1) and 2)\n\n");
fill(A, B);
printf(" <Matrix A>\n\n");
print(A);
printf("\n");
printf(" <Matrix B>\n\n");
print(B);
printf("\n");
printf(" <Matrix C>\n\n");
printf(" -- standard algorithm --\n\n");
standard(A, B, C);
return 0;
}-
result
- 4X4 matrix
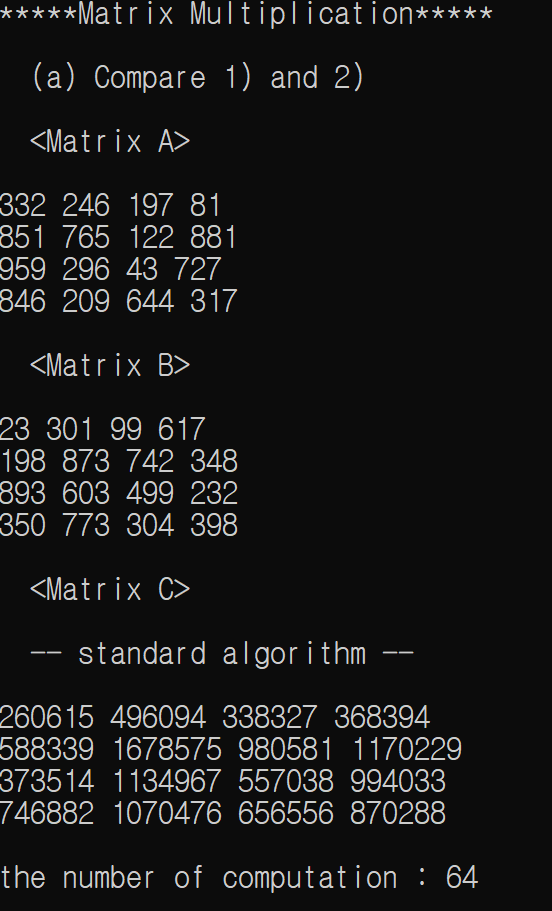
- 8x8 matrix

recursion을 사용하지 않은 알고리즘으로 n x n 행렬 곱샘 수행 시간 복잡도는 n^3 입니다.
Recursion algorithm : strassen algorithm
메인 함수와 매트릭스에 값을 채우는 함수는 위 표준 알고리즘 코드와 동일합니다.
#define _CRT_SEUCRE_NO_WARNINGS
#include <stdio.h>
#include<stdlib.h>
#include<time.h>
#define N 4
int fill(int **A, int **B) {
int i, j;
srand((unsigned)time(NULL));
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
A[i][j] = rand() % 1000;
}
}
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
B[i][j] = rand() % 1000;
}
}
return 0;
}
int print(int **List) {
int i, j;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
printf("%d ", List[i][j]);
}
printf("\n");
}
return 0;
}
int standard(int **A, int **B, int **C) {
int i, j, k;
int computation = 0;
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
C[i][j] = 0;
for (k = 0; k < N; k++) {
C[i][j] += A[i][k] * B[k][j];
computation++;
}
}
}
print(C);
printf("\n");
printf("the number of computation : %d\n", computation);
return 0;
}
void matrix_sum(int n, int** A, int** B, int** C)
{
int i, j;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
C[i][j] = A[i][j] * B[i][j];
}
}
}
void matrix_subtract(int n, int** A, int** B, int** C)
{
int i, j;
for (i = 0; i < n; i++) {
for (j = 0; j < n; j++) {
C[i][j] = A[i][j] - B[i][j];
}
}
}
int strassen(int n, int **A, int **B, int **C) {
if (n == 2) {
standard(A, B, C);
}
else {
int i, j, row, col;
int** a11 = (int**)malloc(sizeof(int*) * N / 2);
int** a12 = (int**)malloc(sizeof(int*) * N / 2);
int** a21 = (int**)malloc(sizeof(int*) * N / 2);
int** a22 = (int**)malloc(sizeof(int*) * N / 2);
int** b11 = (int**)malloc(sizeof(int*) * N / 2);
int** b12 = (int**)malloc(sizeof(int*) * N / 2);
int** b21 = (int**)malloc(sizeof(int*) * N / 2);
int** b22 = (int**)malloc(sizeof(int*) * N / 2);
int** c11 = (int**)malloc(sizeof(int*) * N / 2);
int** c12 = (int**)malloc(sizeof(int*) * N / 2);
int** c21 = (int**)malloc(sizeof(int*) * N / 2);
int** c22 = (int**)malloc(sizeof(int*) * N / 2);
int** m1 = (int**)malloc(sizeof(int*) * N / 2);
int** m2 = (int**)malloc(sizeof(int*) * N / 2);
int** m3 = (int**)malloc(sizeof(int*) * N / 2);
int** m4 = (int**)malloc(sizeof(int*) * N / 2);
int** m5 = (int**)malloc(sizeof(int*) * N / 2);
int** m6 = (int**)malloc(sizeof(int*) * N / 2);
int** m7 = (int**)malloc(sizeof(int*) * N / 2);
int** temp1 = (int**)malloc(sizeof(int*) * N / 2);
int** temp2 = (int**)malloc(sizeof(int*) * N / 2);
for (i = 0; i < n / 2; i++) {
a11[i] = (int*)malloc(sizeof(int) * n / 2);
a12[i] = (int*)malloc(sizeof(int) * n / 2);
a21[i] = (int*)malloc(sizeof(int) * n / 2);
a22[i] = (int*)malloc(sizeof(int) * n / 2);
b11[i] = (int*)malloc(sizeof(int) * n / 2);
b12[i] = (int*)malloc(sizeof(int) * n / 2);
b21[i] = (int*)malloc(sizeof(int) * n / 2);
b22[i] = (int*)malloc(sizeof(int) * n / 2);
c11[i] = (int*)malloc(sizeof(int) * n / 2);
c12[i] = (int*)malloc(sizeof(int) * n / 2);
c21[i] = (int*)malloc(sizeof(int) * n / 2);
c22[i] = (int*)malloc(sizeof(int) * n / 2);
m1[i] = (int*)malloc(sizeof(int) * n / 2);
m2[i] = (int*)malloc(sizeof(int) * n / 2);
m3[i] = (int*)malloc(sizeof(int) * n / 2);
m4[i] = (int*)malloc(sizeof(int) * n / 2);
m5[i] = (int*)malloc(sizeof(int) * n / 2);
m6[i] = (int*)malloc(sizeof(int) * n / 2);
m7[i] = (int*)malloc(sizeof(int) * n / 2);
temp1[i] = (int*)malloc(sizeof(int) * n / 2);
temp2[i] = (int*)malloc(sizeof(int) * n / 2);
}
row = 0, col = 0;
for (i = 0; i < n; i++) {
col = 0;
for (j = 0; j < n; j++) {
if (i < n / 2 && j < n / 2) {
a11[i][j] = A[i][j];
b11[i][j] = B[i][j];
temp1[i][j] = 0;
temp2[i][j] = 0;
c11[i][j] = 0;
c12[i][j] = 0;
c21[i][j] = 0;
c22[i][j] = 0;
}
else if (i >= n / 2 && j < n / 2) {
a21[row][j] = A[i][j];
b21[row][j] = B[i][j];
}
else if (i < n / 2 && j >= n / 2) {
a12[i][col] = A[i][j];
b12[i][col] = B[i][j];
}
else if (i >= n / 2 && j >= n / 2) {
a22[row][col] = A[i][j];
b22[row][col] = B[i][j];
}
if (j >= n / 2) col++;
}
if (i >= n / 2) row++;
}
row = 0, col = 0;
matrix_sum(n / 2, a11, a22, temp1);
matrix_sum(n / 2, b11, b22, temp2);
strassen(n / 2, temp1, temp2, m1);
matrix_sum(n / 2, a21, a22, temp1);
strassen(n / 2, temp1, b11, m2);
matrix_subtract(n / 2, b12, b22, temp2);
strassen(n / 2, a11, temp2, m3);
matrix_subtract(n / 2, b21, b11, temp2);
strassen(n / 2, a22, temp2, m4);
matrix_sum(n / 2, a11, a12, temp1);
strassen(n / 2, temp1, b22, m5);
matrix_subtract(n / 2, a21, a11, temp1);
matrix_sum(n / 2, b11, b12, temp2);
strassen(n / 2, temp1, temp2, m6);
matrix_subtract(n / 2, a12, a22, temp1);
matrix_sum(n / 2, b21, b22, temp2);
strassen(n / 2, temp1, temp2, m7);
matrix_sum(n / 2, m1, m4, temp1);
matrix_subtract(n / 2, temp1, m5, temp2);
matrix_sum(n / 2, temp2, m7, c11);
matrix_sum(n / 2, m3, m5, c12);
matrix_sum(n / 2, m2, m4, c21);
matrix_sum(n / 2, m1, m3, temp1);
matrix_subtract(n / 2, temp1, m2, temp2);
matrix_sum(n / 2, temp2, m6, c22);
for (i = 0; i < n; i++) {
col = 0;
for (j = 0; j < n; j++) {
if (i < n / 2 && j < n / 2) {
C[i][j] = c11[i][j];
}
else if (i >= n / 2 && j < n / 2) {
C[i][j] = c21[row][j];
}
else if (i < n / 2 && j >= n / 2) {
C[i][i] = c12[i][col];
}
else if (i >= n / 2 && j >= n / 2) {
C[i][j] = c22[row][col];
}
if (j >= n / 2) col++;
}
if (i >= n / 2) row++;
}
for (i = 0; i < n / 2; i++) {
free(a11[i]); free(a12[i]); free(a21[i]); free(a22[i]);
free(b11[i]); free(b12[i]); free(b21[i]); free(b22[i]);
free(c11[i]); free(c12[i]); free(c21[i]); free(c22[i]);
free(temp1); free(temp2);
free(m1[i]); free(m2[i]); free(m3[i]); free(m4[i]); free(m5[i]); free(m6[i]); free(m7[i]);
}
free(a11); free(a12); free(a21); free(a22);
free(b11); free(b12); free(b21); free(b22);
free(c11); free(c12); free(c21); free(c22);
free(temp1); free(temp2);
free(m1); free(m2); free(m3); free(m4); free(m5); free(m6); free(m7);
}
return 0;
}
int main() {
int **A = (int**)malloc(sizeof(int*) * N);
int **B = (int**)malloc(sizeof(int*) * N);
int **C = (int**)malloc(sizeof(int*) * N);
for (int t = 0; t < N; t++) {
A[t] = (int*)malloc(sizeof(int) * N);
B[t] = (int*)malloc(sizeof(int) * N);
C[t] = (int*)malloc(sizeof(int) * N);
}
printf("*****Matrix Multiplication*****\n\n");
printf(" (a) Compare 1) and 2)\n\n");
fill(A, B);
printf(" <Matrix A>\n\n");
print(A);
printf("\n");
printf(" <Matrix B>\n\n");
print(B);
printf("\n");
printf(" <Matrix C>\n\n");
printf(" -- standard algorithm --\n\n");
standard(A, B, C);
printf("\n -- recursion algorithm --\n\n");
strassen(N, A, B, C);
return 0;
}- strassen algorithm explanation
1960년대 후반, strassen은 표준 알고리즘 보다 시간 복잡도가 적은 곱셈 행렬 알고리즘을 제안했습니다.
- Matrix C is from multiplication of matrix A and B. A size of A and B is 2n x 2n (n is positive integer). If the size of A and B is not 2n, the empty field shoudl be filled by 0 to be shape of 2n x 2n.
- Each matrix A, B and C can be dvided into 4 parts recursively.

3. If a size of sub matrix through dividing the matrix becomes 2, the phase of dividing the matrix is finished and then compute the elements

4. Each sub matrix is computed, following the algorithm.

5. The matrix C which is result of A x B has elements like this.

'프로그래밍 언어 > C' 카테고리의 다른 글
| C/C++ programming tutorial (0) | 2021.03.02 |
|---|---|
| Hash Table : open addressing (0) | 2021.02.15 |
| 연결리스트 삽입, 삭제, 출력 Linked List insert delete print 구현하기 (0) | 2021.02.15 |
| 합병 정렬 : Merge Sort 내림차순으로 구현하기 (0) | 2021.02.15 |
| 버블 정렬 Bubble Sort 오름차순으로 구현하기 (0) | 2021.02.15 |



